注：此博客改编自《数据结构与算法分析：C语言描述》中二项队列一节，如有设计不当之处还请指出。

二项队列的结构

二项队列(Binomial Queue)是一种可以实现：
$(1)$向其中添加元素；
$(2)$删除、获取其中的最小(最大)元素；
$(3)$合并两个二项队列的数据结构。
和它具有相同功能的有左式堆(左偏树)(Leftist Heap)和斜堆(Skew Heap)。但是它们的所有操作都花费$O(logN)$时间，而二项队列的插入操作只需常数时间。
不同于左偏树和斜堆，二项队列一般地由具有堆序性质的多棵树构成，即森林。每棵堆序树称为二项树(Binomial Tree),它们具有下图所示的结构：

下面的每个数字表示图中二项树的高度。记深度为$k$的二项树为$B_k$。在$B_4$中，考察图中每一层的节点数，可以发现符合二项系数$(1,4,6,4,1)$。一般地，高度为$k$的的二项树在深度为$d$处的节点总数是$C_d^k$。
回到二项队列的结构：设一个二项队列包含$N$个元素，那么将$N$表示为它的二进制形式，二项队列便由$popcount(N)$个二项树组成，其中$popcount(N)$表示$N$的二进制表示中$1$的个数。每个二项树对应一个2的幂：例如，一个二项队列包含$13$个元素，将$13$写为二进制$1101_{(2)}=8+4+1$，那么这个二项队列便由深度为$3、2、0$的二项树组成(即$B_3,B_2,B_0$)。

二项队列的操作

求最小(最大)元素

以求最小元素为例。那么，每棵上述的二项树都应该满足小根堆性质。因此，我们可以从所有二项树，最多$logN$棵中求得最小元。因此求得最小元的时间复杂度为$O(logN)$。

合并两个二项队列

由于插入元素可以转化为合并一个二项队列和一个单独的节点，因此我们只需要像左偏树一样解决合并问题即可。

现在要合并如图所示的两个二项队列$H_1、H_2$。合并是通过类似二进制相加的方法完成的：
$(1)$考察两个二项队列的$B_0$部分，$H_2$有$B_0$而$H_1$没有，因此合成后的二项队列的$B_0$就是$H_2$的$B_0$。
$(2)$考察$B_1$部分，两个二项队列均有$B_1$，比较二者的根值，$H_2$的根值较小，为$14$，因此为了保持小根堆的性质，我们将$H_2$的$B_1$加入到$H_1$的上面，如下图；
$(3)$考察$B_2$部分，此时不仅$H_1,H_2$有$B_2$，刚才在$(2)$中我们像进位一样得到了一个$B_2$，因此现在共有三个$B_2$。将其中两个合并(同样要保持小根堆性质，这里选择除了进位得到的那两个合并)，得到一个$B_3$,剩下一个(这里选择刚才进位得到的)作为新二项队列的$B_2$部分。
$(4)$原先的二项队列没有$B_3$,但刚才$(3)$中进位得到了一个，将它作为新二项队列的$B_3$部分。
经过上述过程，两个二项队列合并为一个。

图中的颜色对应了合并前后各数据的位置。

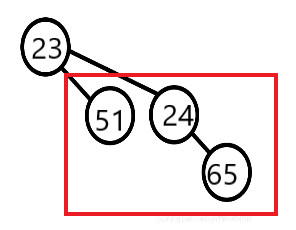
删除最小(最大)元素

删除最小元素，需要先确定最小元素在哪一棵二项树上，这可以通过$O(logN)$的遍历确定。然后将这棵二项树的堆顶抹去：

如图所示，若这个二项树是最小元素所在的二项树，去掉堆顶元素后红框圈起的部分变成了一个$B_1$，可以视作一个新的二项队列，那么只需要将这个新的二项队列$H’’$与原二项队列除掉这棵二项树得到的$H’$合并即可。来看一个例子：

在刚才合并得到的二项队列中，我们要删除最小元$12$，先找到它所在的二项树$B_3$:

去掉$12$，得到一个新的二项队列：

合并它和剩下的

即可。合并结果：

(由于涉及进位，结果不唯一)

代码实现

这里采用C++的一些语法。
首先是类型声明：
由于我们在删除操作后需要堆顶元素的儿子节点，所以我们采用链表式的结构：每个节点记录它的第一个儿子节点和下一个兄弟节点，代码如下：

struct BinNode
{
	int Element;//存放数据
	BinNode *FirstChild;//第一个儿子
	BinNode *NextSibling;//下一个兄弟节点
};

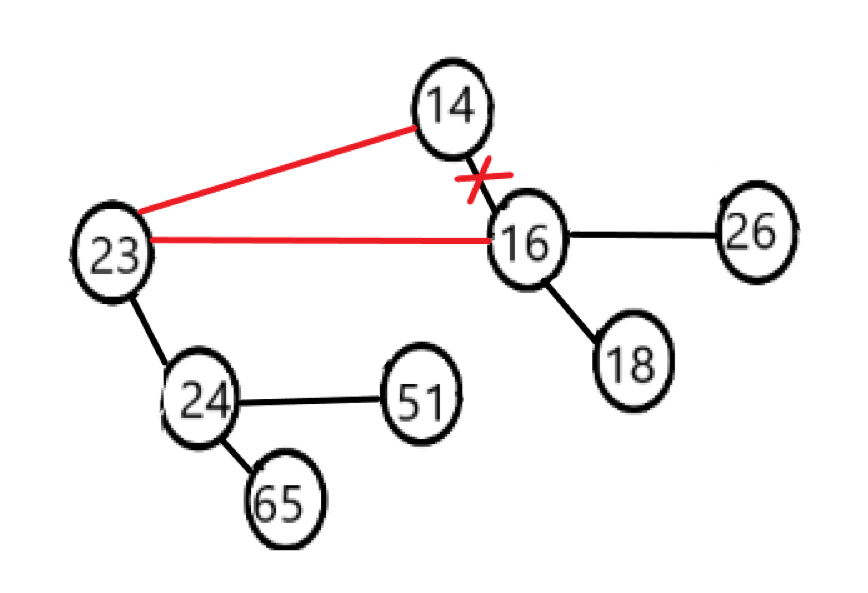
下图是链表式的存法：

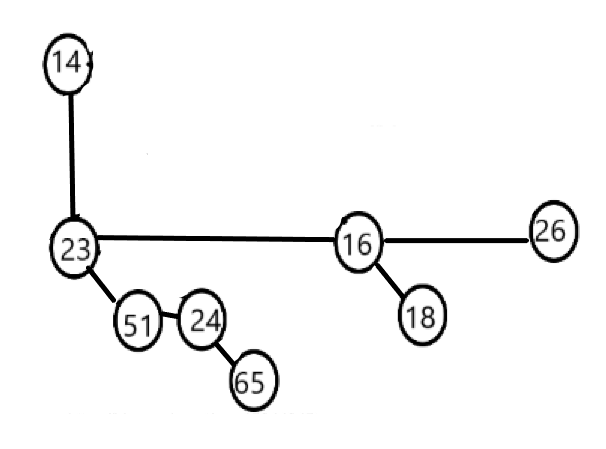
结构如图所示。横线表示下一个兄弟节点的指针，斜线表示第一个儿子节点指针。图中画的儿子按子树从大到小排列，这样做可以保证在合成两个相同大小的二项树时保持其原有的性质，见下面例子的图解。

再用一个结构体将所有二项树整合起来：

struct BinQueue
{
	int CurrentSize;
	BinNode *Trees[18];
};

$CurrentSize$表示当前二项队列的大小，$18$大小的二项树数组可以存放$10^5$级别的数据。$(2^0+2^1+..+2^{17}=262143>10^5)$

初始化一个空的二项队列的函数：

BinQueue* Initialize()
{
	BinQueue *Init = (BinQueue*)malloc(sizeof(BinQueue));
	Init->CurrentSize = 0;
	for(int i=0;i<MaxTrees;i++)
		Init->Trees[i] = NULL;
	return Init;
}

在合并两个二项队列的时候，我们总是合并两个相同大小的二项树，代码如下：

BinNode* CombineTrees(BinNode *T1,BinNode *T2)
{
	if(T1->Element > T2->Element)
		return CombineTrees(T2,T1);
	T2->NextSibling = T1->FirstChild;
	T1->FirstChild = T2;
	return T1;
}

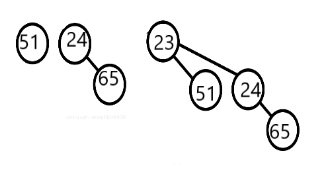
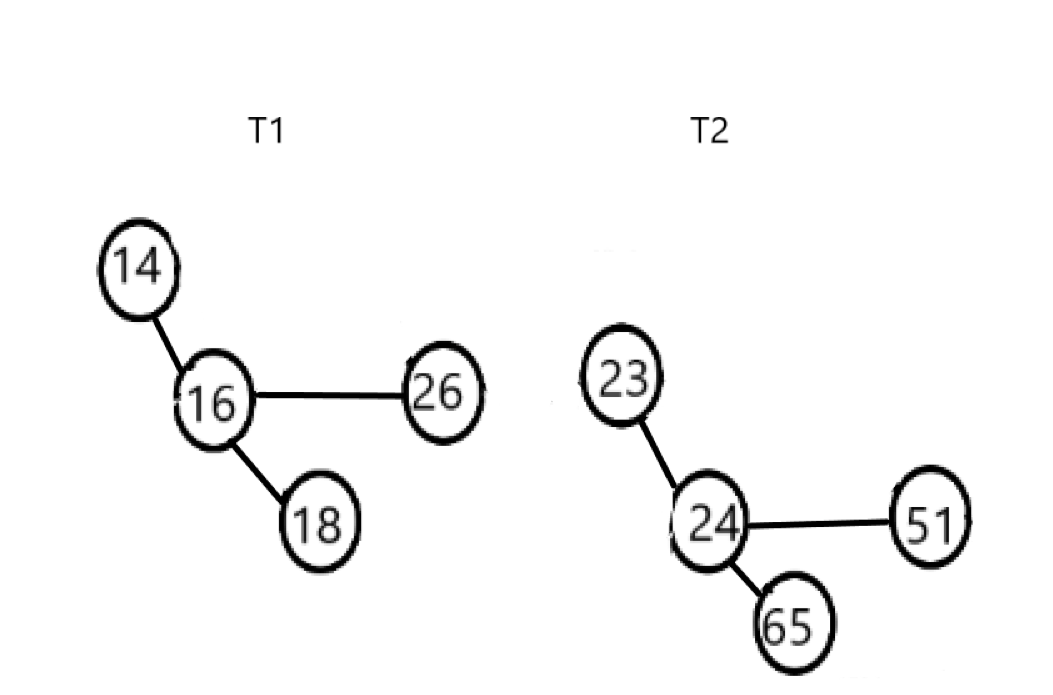
我们假设$T_1$的根节点较小，因此当$T_1$的根节点大时交换两棵二项树。合并时，将$T_1$的第一个儿子设为$T_2$的根，同时让$T_2$的下一个兄弟节点指向原先$T_1$的儿子节点。

在合并过程中，其中根较大的二项树成为了另一个二项树的第一个儿子，这也保持了儿子从大到小排列的性质。

然后是合并的总代码，代码较长，但主要是对是否有空树和进位的$8$种情况的讨论：

BinQueue* Merge(BinQueue *H1,BinQueue *H2)//将H2合并到H1上
{
	BinNode *T1,*T2,*Carry  = NULL;
	int i,j;
	
	H1->CurrentSize += H2->CurrentSize;//更新大小
	for(i = 0,j = 1;j <= H1->CurrentSize;i++,j <<= 1)
	{
		T1 = H1->Trees[i];
		T2 = H2->Trees[i];//两个对应的二项树
		
		switch(!!T1 + 2 * !!T2 + 4 * !!Carry)//见下面的说明
		{
			case 0:
				break;
			case 1:
				break;
			case 2:
				H1->Trees[i] = T2;
				H2->Trees[i] = NULL;
				break;
			case 3:
				Carry = CombineTrees(T1,T2);
				H1->Trees[i] = H2->Trees[i] = NULL;
				break;
			case 4:
				H1->Trees[i] = Carry;
				Carry = NULL;
				break;
			case 5:
				Carry = CombineTrees(T1,Carry);
				H1->Trees[i] = NULL;
				break;
			case 6:
				Carry = CombineTrees(T2,Carry);
				H2->Trees[i] = NULL;
				break;
			case 7:
				H1->Trees[i] = Carry;
				Carry = CombineTrees(T1,T2);
				break;
				
		}
	}
	return H1;
}

switch中的语句是对讨论内容的简写。它基于这样的事实：当$T == NULL$，$!\ T =1,!!\ T = 0$；反之，当$T$不为$NULL$,$!!\ T=1$。因此switch中的内容是用三个$T_1,T_2,Carry$(进位)编码的一个二进制数$(CT_2T_1)_{(2)}$.
进一步对讨论的内容说明：
case $0:000$，此时三棵树$(Carry,T_1,T_2)$均为空，跳过；
case $1:001$，此时$T_1$非空，其他均为空，由于就是要将$T_2$合并到$T_1$上，跳过即可。
case $2:010$，此时仅有$T_2$非空，将它合并到$T_1$上后设为$NULL$。
case $3:011$，此时$T_1,T_2$非空，把它们合并后进位。
case $4:100$，此时仅有进位，把进位保留在这一位上，并且设为$NULL$。
case $5:101$，此时进位和$T_1$非空，把进位和$T_1$合并作为新的进位。
case $6:110$，与case $5$类似，把进位和$T_2$合并作为新的进位。
case $7:111$，此时三棵树都非空，这里选择将进位得来的树保留在此位置，剩下两棵树作为新的进位。
最后返回$H_1$即可。

有了合并的代码，我们可以写出插入的代码：

void Insert(BinQueue *H,int X)
{
	BinQueue *SingleNode = Initialize();
	SingleNode->Trees[0] = (BinNode*)malloc(sizeof(BinNode));
	SingleNode->Trees[0]->Element = X;
	SingleNode->Trees[0]->FirstChild = SingleNode->Trees[0]->NextSibling = NULL;
	SingleNode->CurrentSize = 1;
	Merge(H,SingleNode);
}

最后是删除部分：

int DeleteMin(BinQueue *H)
{
	int i,j;
	int MinTree;
	BinQueue *DeletedQueue;
	BinNode *DeletedTree,*OldRoot;
	int MinItem = INT_MAX;
	for(int i=0;i<MaxTrees;i++)
	{
		if(H->Trees[i] && H->Trees[i]->Element < MinItem)
		{
			MinItem = H->Trees[i]->Element;
			MinTree = i;
		}
	}//找出最小元素所在的二项树
	
	DeletedTree = H->Trees[MinTree];
	OldRoot = DeletedTree;
	DeletedTree = DeletedTree->FirstChild;//指向儿子们
	free(OldRoot);//删掉根节点
	
	DeletedQueue = Initialize();//删除最小元后的新的二项队列H''
	DeletedQueue->CurrentSize = (1<<MinTree)-1;
	//原先这个二项树有2的(MinTree)次方个元素，删掉最小元
	for(j=MinTree-1;j>=0;j--)
	{
		DeletedQueue->Trees[j] = DeletedTree;
		DeletedTree = DeletedTree->NextSibling;
		DeletedQueue->Trees[j]->NextSibling = NULL;
	}//用链表遍历剩下的儿子们，添加到新的H''中
	
	H->Trees[MinTree] = NULL;//除掉最小元所在的二项树
	H->CurrentSize -= DeletedQueue->CurrentSize+1;//更新大小，减去H''的大小再+1(最小元)
	Merge(H,DeletedQueue);//合并即可
	
	return MinItem;
}

实现细节见注释。

例题：洛谷P1456 Monkey King

题目链接

题目大意：

有$N$只猴子，每只猴子有一个强壮值，每只猴子最开始不认识；给定$M$次询问，每次询问让两只猴子所在的猴群猴子中最强壮的两个打架，打架后最强壮的两只猴子强壮值除以二(向下取整)，同时两群猴子会互相认识。对于每次询问，输出合并后这群猴子最强壮的那个的强壮值。如果两群猴子一开始就认识，输出$-1$。
注：多组数据。

题解：

显然这是一个可并堆的问题，同时为了维护两个猴子是否互相认识我们需要采用并查集。一开始开$N$个二项队列维护，按照题意模拟即可。
注意前面的例子都是小根堆，这里要改成大根堆，找最小元和合并两个二项树的时候要注意顺序。在上面例程的基础上还增加了一个获取最大值而不删除的函数。

$Code:$

#include<cstdio>
#include<cstdlib>
#include<climits>

const int MaxTrees = 18;
const int MAXN = 1E5+1;

int fa[MAXN];
int findfa(int x)
{
	return fa[x] == x?fa[x]:fa[x] = findfa(fa[x]);
}
void unity(int x,int y)
{
	fa[findfa(x)] = findfa(y);
}
struct BinNode
{
	int Element;
	BinNode *FirstChild;
	BinNode *NextSibling;
};

struct BinQueue
{
	int CurrentSize;
	BinNode *Trees[18];
};

BinNode* CombineTrees(BinNode *T1,BinNode *T2)
{
	if(T1->Element < T2->Element)
		return CombineTrees(T2,T1);
	T2->NextSibling = T1->FirstChild;
	T1->FirstChild = T2;
	return T1;
}

BinQueue* Merge(BinQueue *H1,BinQueue *H2)
{
	BinNode *T1,*T2,*Carry  = NULL;
	int i,j;
	
	H1->CurrentSize += H2->CurrentSize;
	for(i = 0,j = 1;j <= H1->CurrentSize;i++,j <<= 1)
	{
		T1 = H1->Trees[i];
		T2 = H2->Trees[i];
		
		switch(!!T1 + 2 * !!T2 + 4 * !!Carry)
		{
			case 0:
				break;
			case 1:
				break;
			case 2:
				H1->Trees[i] = T2;
				H2->Trees[i] = NULL;
				break;
			case 3:
				Carry = CombineTrees(T1,T2);
				H1->Trees[i] = H2->Trees[i] = NULL;
				break;
			case 4:
				H1->Trees[i] = Carry;
				Carry = NULL;
				break;
			case 5:
				Carry = CombineTrees(T1,Carry);
				H1->Trees[i] = NULL;
				break;
			case 6:
				Carry = CombineTrees(T2,Carry);
				H2->Trees[i] = NULL;
				break;
			case 7:
				H1->Trees[i] = Carry;
				Carry = CombineTrees(T1,T2);
				break;
				
		}
	}
	return H1;
}

BinQueue* Initialize()
{
	BinQueue *Init = (BinQueue*)malloc(sizeof(BinQueue));
	Init->CurrentSize = 0;
	for(int i=0;i<MaxTrees;i++)
		Init->Trees[i] = NULL;
	return Init;
}

int GetMax(BinQueue *H)
{
	int MaxTree;
	int MaxItem = 0;
	for(int i=0;i<MaxTrees;i++)
	{
		if(H->Trees[i] && H->Trees[i]->Element > MaxItem)
		{
			MaxItem = H->Trees[i]->Element;
			MaxTree = i;
		}
	}
	return MaxItem;
}
int GetMaxId(BinQueue *H)
{
	int MaxTree;
	int MaxItem = 0;
	for(int i=0;i<MaxTrees;i++)
	{
		if(H->Trees[i] && H->Trees[i]->Element > MaxItem)
		{
			MaxItem = H->Trees[i]->Element;
			MaxTree = i;
		}
	}
	return H->Trees[MaxTree]->id;
}
int DeleteMax(BinQueue *H)
{
	int MaxTree;
	BinQueue *DeletedQueue;
	BinNode *DeletedTree,*OldRoot;
	int MaxItem = 0;
	for(int i=0;i<MaxTrees;i++)
	{
		if(H->Trees[i] && H->Trees[i]->Element > MaxItem)
		{
			MaxItem = H->Trees[i]->Element;
			MaxTree = i;
		}
	}
	

	DeletedTree = H->Trees[MaxTree];
	OldRoot = DeletedTree;
	DeletedTree = DeletedTree->FirstChild;

	free(OldRoot);

	DeletedQueue = Initialize();
	DeletedQueue->CurrentSize = (1<<MaxTree)-1;
	for(int j=MaxTree-1;j>=0;j--)
	{
		DeletedQueue->Trees[j] = DeletedTree;
		DeletedTree = DeletedTree->NextSibling;
		DeletedQueue->Trees[j]->NextSibling = NULL;
	}
	
	H->Trees[MaxTree] = NULL;
	H->CurrentSize -= DeletedQueue->CurrentSize+1;
	Merge(H,DeletedQueue);
	
	return MaxItem;
}

void Insert(BinQueue *H,int X)
{
	BinQueue *SingleNode = Initialize();
	SingleNode->Trees[0] = (BinNode*)malloc(sizeof(BinNode));
	SingleNode->Trees[0]->Element = X;
	SingleNode->Trees[0]->FirstChild = SingleNode->Trees[0]->NextSibling = NULL;
	SingleNode->CurrentSize = 1;
	Merge(H,SingleNode);
}
int main()
{
	int n,m,x;
	BinQueue *H[MAXN];
	while(scanf("%d",&n) != EOF)
	{
		for(int i=1;i<=n;i++)
		{
			fa[i] = i;
			H[i] = Initialize();
			scanf("%d",&x);
			Insert(H[i],x);
		}
		scanf("%d",&m);
		for(int i=1;i<=m;i++)
		{
			int x,y;
			scanf("%d%d",&x,&y);
			x = findfa(x);
			y = findfa(y);
			if(x == y)
			{
				printf("-1\n");
				continue;
			}
			int vx = DeleteMax(H[x]) >> 1;
			int vy = DeleteMax(H[y]) >> 1;
			unity(x,y);
			H[x] = Merge(H[x],H[y]);
			Insert(H[x],vx);
			Insert(H[x],vy);
			H[y] = H[x];
			printf("%d\n",GetMax(H[x]));
		}
	}
	return 0;
}

Castria的博客

二项队列介绍及其实现