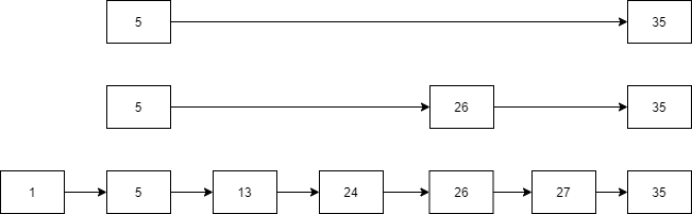
跳表(Skip List)是在链表基础上进行改进的一种有序的数据结构,它为了便于查找,在插入过程中随机地将一些元素提升为高度为1~r的索引,以此来加快之后的操作。索引可以分为多层,一般而言,层数越高的索引个数越少。下面的图是一个跳表示例(隐去表头,上面的为高层)
为了方便下面对代码实现的说明,先给出各数据类型的定义。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| template<typename T>
class skiplist
{
private:
static constexpr int MAX_LEVEL = 16;
static constexpr double P = 0.6;
std::random_device rd;
std::mt19937 gen;
std::uniform_real_distribution<> dis;
struct node
{
T data;
node *next[MAX_LEVEL+1];
node()
{
for(int i=1;i<=MAX_LEVEL;i++)
next[i] = NULL;
}
};
node *head;
public:
skiplist()
{
head = new node;
gen = std::mt19937(rd());
dis = std::uniform_real_distribution<> (0,1);
}
};
|
node型的next[i]表示每个结点第i层的后继结点。与图中分开画的每层不同,存储时每一列结点存在一个node中,如图中的值为5的结点的next[3]指向35,next[2]指向26,next[1]指向13。
(1)查找操作
我们假设跳表已经有如图所示的结构。假设现在要查找27,那么查找将沿如下路径进行:
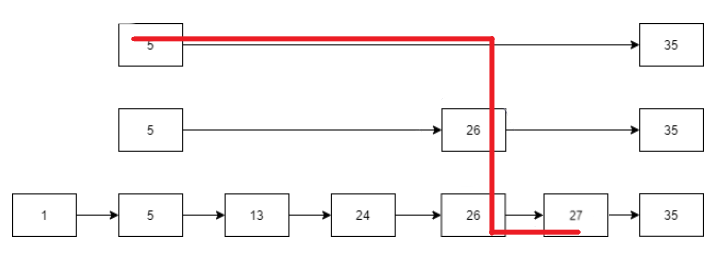
首先初始化一个指针p指向最高层i=3,不断遍历直至该指针在i层的下一个元素>=查找元素x,如,在第三层执行该操作使得指针指向5结束;此时i–,在第二层继续执行该操作,因此指针最终指向26;在第一层指针指向26,结束。比对p的下一个元素27,发现与待查找元素相等,返回true,否则,若指针为空或不相等,返回false。
代码实现:
1
2
3
4
5
6
7
8
9
| bool find(T x)
{
node *now = head;
for(int i=MAX_LEVEL;i>=1;i--)
while(now->next[i] != NULL && now->next[i]->data<x) now = now->next[i];
if(now->next[1] == NULL) return false;
if(now->next[1]->data != x) return false;
return true;
}
|
代码逻辑与上面的解释基本一致,需要注意的是代码采用了表头,图中未体现。
(2)插入操作
假设链表已具有上面的图示结构。若现在要插入28,并且经过随机化决定将28插入到第1~2层(即高度为2),则插入后应该变为图中这样:
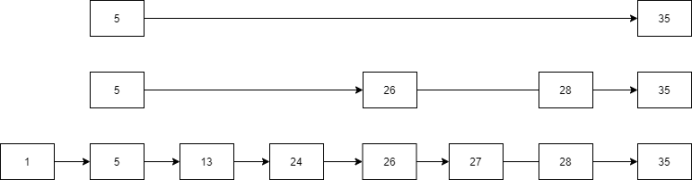
与查找很类似,需要先找到插入的位置。因此经过查找部分的遍历,指针指向了27.不同的是,由于需要修改1~2层的指针,因此需要将每层的,新结点的前驱结点记录下来。如:第2层的前驱节点是26,第1层的前驱节点是27。最后对1~r层的指针进行修改即可,其中r是该节点被随机到的高度。随机化函数采用第一层概率$p_1=q$(记$q=1-p$),第二层概率是$pq$,第三层概率是$p²q,…$当$n→∞$时,易知此数列收敛于$1$.当然实际不允许无穷的层数,用MAX_LEVEL兜底。在测试中$p$在$0.6$左右效果较好。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| int randomLevel()
{
int ret = 1;
while(ret<MAX_LEVEL && dis(gen)<P)
ret++;
return ret;
}
void insert(T x)
{
node *tmp = new node;
tmp->data = x;
node *pre[MAX_LEVEL];
node *now = head;
int level = randomLevel();
for(int i=MAX_LEVEL;i>=1;i--)
{
while(now->next[i] != NULL && now->next[i]->data<x) now = now->next[i];
pre[i] = now;
}
for(int i=level;i>=1;i--)
{
tmp->next[i] = pre[i]->next[i];
pre[i]->next[i] = tmp;
}
}
|
(3)删除操作
与插入很类似,同样记录被删除结点的前驱,使每个被修改的前驱跳过被删除元素指向下一个即可。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| bool remove(T x)
{
node *pre[MAX_LEVEL+1];
node *now = head;
for(int i=MAX_LEVEL;i>=1;i--)
{
while(now->next[i] != NULL && now->next[i]->data<x) now = now->next[i];
pre[i] = now;
}
if(now->next[1] == NULL) return false;
if(now->next[1]->data != x) return false;
for(int i=MAX_LEVEL;i>=1;i--)
pre[i]->next[i] = pre[i]->next[i]->next[i];
return true;
}
|
整个测试程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
| #include<set>
#include<ctime>
#include<cstdio>
#include<random>
template<typename T>
class skiplist
{
private:
static constexpr int MAX_LEVEL = 16;
static constexpr double P = 0.6;
std::random_device rd;
std::mt19937 gen;
std::uniform_real_distribution<> dis;
struct node
{
T data;
node *next[MAX_LEVEL+1];
node()
{
for(int i=1;i<=MAX_LEVEL;i++)
next[i] = NULL;
}
};
node *head;
public:
skiplist()
{
head = new node;
gen = std::mt19937(rd());
dis = std::uniform_real_distribution<> (0,1);
}
int randomLevel()
{
int ret = 1;
while(ret<MAX_LEVEL && dis(gen)<P)
ret++;
return ret;
}
void insert(T x)
{
node *tmp = new node;
tmp->data = x;
node *pre[MAX_LEVEL];
node *now = head;
int level = randomLevel();
for(int i=MAX_LEVEL;i>=1;i--)
{
while(now->next[i] != NULL && now->next[i]->data<x) now = now->next[i];
pre[i] = now;
}
for(int i=level;i>=1;i--)
{
tmp->next[i] = pre[i]->next[i];
pre[i]->next[i] = tmp;
}
}
bool remove(T x)
{
node *pre[MAX_LEVEL+1];
node *now = head;
for(int i=MAX_LEVEL;i>=1;i--)
{
while(now->next[i] != NULL && now->next[i]->data<x) now = now->next[i];
pre[i] = now;
}
if(now->next[1] == NULL) return false;
if(now->next[1]->data != x) return false;
for(int i=MAX_LEVEL;i>=1;i--)
pre[i]->next[i] = pre[i]->next[i]->next[i];
return true;
}
bool find(T x)
{
node *now = head;
for(int i=MAX_LEVEL;i>=1;i--)
while(now->next[i] != NULL && now->next[i]->data<x) now = now->next[i];
if(now->next[1] == NULL) return false;
if(now->next[1]->data != x) return false;
return true;
}
void print()
{
node *now = head->next[1];
while(now != NULL)
{
printf("%d ",now->data);
now = now->next[1];
}
}
};
int main()
{
for(int i=1;i<=10;i++)
{
std::set<int> S;
skiplist<int> L;
double clk1 = clock();
for(int i=100000;i>=1;i--)
L.insert(i);
double clk2 = clock();
for(int i=100000;i>=1;i--)
S.insert(i);
double clk3 = clock();
printf("skiplist:%lf,set:%lf\n",clk2-clk1,clk3-clk2);
}
return 0;
}
|
测试结果:
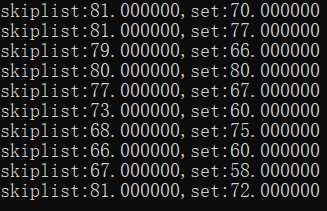
测试中,将跳表与STL的set进行了对比。在插入$10^5$个逆序数据时,跳表与set的运行时间相近,与理论上$log\ n$的复杂度吻合。



