题意
给定一个字符串 ($s$) 和一个字符模式 ($p$) ,实现一个支持 $’?’$ 和 $’*’$ 的通配符匹配。
1
2
| '?' 可以匹配任何单个字符。
'*' 可以匹配任意字符串(包括空字符串)。
|
如:
$”ab”$可以匹配$”adceb”$(第一个$$为空,第二个$$为$dce$)
限制字母表为小写字母。
(另有LeetCode 10.正则表达式匹配与其相似,但更像正则表达式)
题解
因为这学期正好在学形式语言与自动机这门课,这道题显然是一个正则表达式的问题,就尝试模拟了一下正则表达式转$\epsilon-NFA$。(虽然最后跑出来特别慢,但好处是直接按部就班走,不需要动脑子)
先构造出空串$\epsilon$的$NFA:$
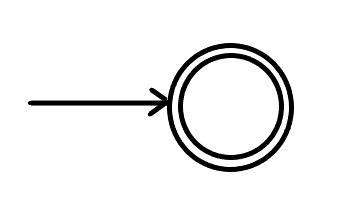
对于每个输入字符,在原有的$NFA$上进行修改,产生一个新的自动机。
考虑给定字符$a$的三种情况:
$(1)$$a$是小写字母。
构造新自动机的方法很简单:使原有的终结状态$F_0$变为非终结状态,让$F_0$经$a$转移到新创建的终结状态$F’$.
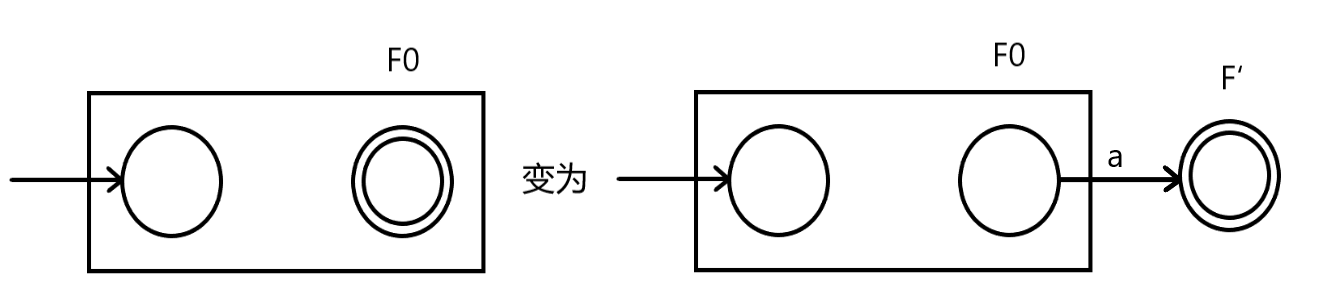
$(2)a$是$’?’$。
与$(1)$类似,只不过任意字符都能使其进入新的终结状态。在这里直接用’?’代替。
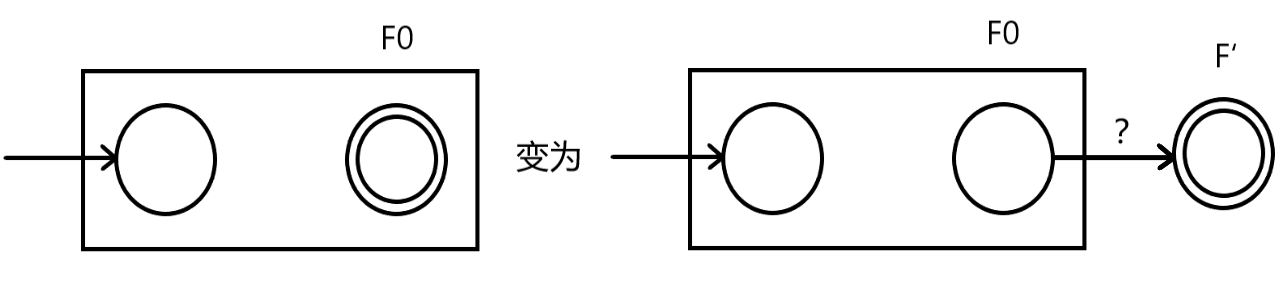
$(3)a$是$’‘$。
由于’‘可以代替零个及以上的字符,那么它就可以不读取字符经空转移到下一个状态,或用任意字符转移到自身。新自动机如下:
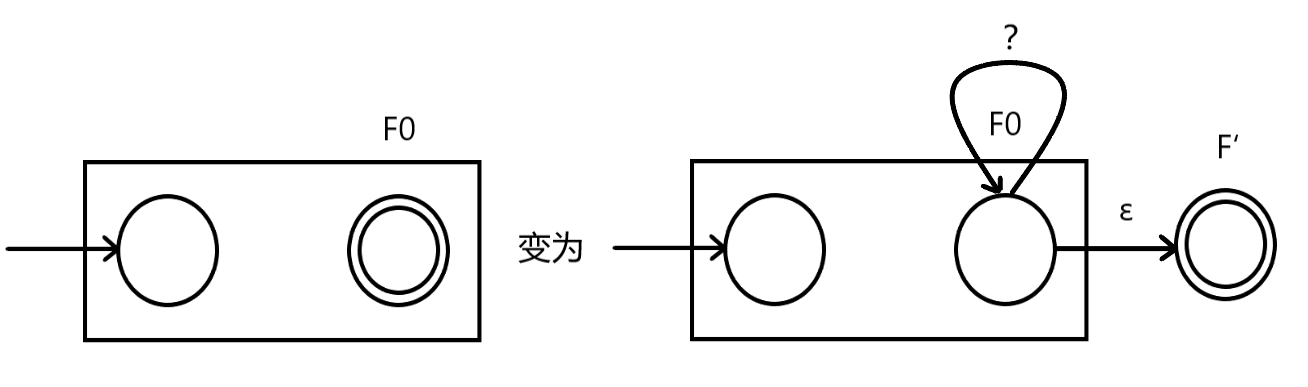
代码
类成员:
1
2
3
4
5
6
7
8
9
10
11
12
| class NFA {
struct state {
bool star;
char ch;
state *next;
state() {
star = false;
next = nullptr;
}
};
state *start, *final;
}
|
其中:
$(1)$$state$为$NFA$中的状态。
$(2)$若$star==true$,说明该状态可以在自身进行任意次转移;
$(3)$由于一个状态只能经由一种字符($’?’$也包括在内)转移到下一个状态,所以只用一个$char$型的$ch$来保存这个使其转移的字符。
$(4)next$是指向转移的下一个状态的指针。
$(5)start$和$final$分别指向起始状态和终止状态。
用一个新字符更新自动机,与上面阐述的思路相同。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void addState(char op) {
state *tmp = new state;
if((op >= 'a' && op <= 'z') || op == '?') {
final->star = false;
final->ch = op;
final->next = tmp;
final = final->next;
}
else {
final->star = true;
final->ch = '#';
final->next = tmp;
final = final->next;
}
}
|
取$\epsilon-$闭包,用$set$保存过程中的状态集合(所以很慢):
1
2
3
4
5
6
7
8
9
10
11
| set<state*> ECLOSE(set<state*> S) {
set<state*> ret = S;
for(auto it = S.begin(); it != S.end(); ++it) {
state *p = *it;
while(p->ch == '#') {
p = p->next;
ret.insert(p);
}
}
return ret;
}
|
匹配过程:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| bool isMatch(string str) {
set<state*> S;
S.insert(start);
S = ECLOSE(S);
for(int i = 0; i < str.size(); i++) {
set<state*> tmp;
for(auto it = S.begin(); it != S.end(); ++it) {
if((*it)->star) tmp.insert(*it);
if((*it)->ch == str[i] || (*it)->ch == '?') tmp.insert((*it)->next);
}
S = ECLOSE(tmp);
}
for(auto it = S.begin(); it != S.end(); it++) {
if((*it) == final) return true;
}
return false;
}
|
顺便附上$\epsilon-NFA$的匹配过程(来源:Automata Theory,Languages,and Computation第三版):


串$w$被接受当且仅当$\delta(q_0,w)$与终结状态集$F$的交集不为空。
完整代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| class Solution {
class NFA {
struct state {
bool star;
char ch;
state *next;
state() {
star = false;
next = nullptr;
}
};
state *start, *final;
set<state*> ECLOSE(set<state*> S) {
set<state*> ret = S;
for(auto it = S.begin(); it != S.end(); ++it) {
state *p = *it;
while(p->ch == '#') {
p = p->next;
ret.insert(p);
}
}
return ret;
}
public:
NFA() {
start = final = new state;
}
void addState(char op) {
state *tmp = new state;
if((op >= 'a' && op <= 'z') || op == '?') {
final->star = false;
final->ch = op;
final->next = tmp;
final = final->next;
}
else {
final->star = true;
final->ch = '#';
final->next = tmp;
final = final->next;
}
}
bool isMatch(string str) {
set<state*> S;
S.insert(start);
S = ECLOSE(S);
for(int i = 0; i < str.size(); i++) {
set<state*> tmp;
for(auto it = S.begin(); it != S.end(); ++it) {
if((*it)->star) tmp.insert(*it);
if((*it)->ch == str[i] || (*it)->ch == '?') tmp.insert((*it)->next);
}
S = ECLOSE(tmp);
}
for(auto it = S.begin(); it != S.end(); it++) {
if((*it) == final) return true;
}
return false;
}
};
public:
bool isMatch(string s, string p) {
NFA N;
for(int i = 0; i < p.size(); i++)
N.addState(p[i]);
return N.isMatch(s);
}
};
|





